Post Correspondence Problem

Post Correspondence Problem is a popular undecidable problem that was introduced by Emil Leon Post in 1946. It is simpler than Halting Problem. In this problem we have N number of Dominos (tiles). The aim is to arrange tiles in such order that string made by Numerators is same as string made by Denominators. In simple words, lets assume we have two lists both containing N words, aim is to find out concatenation of these words in some sequence such that both lists yield same result. Let’s try understanding this by taking two lists A and B

A=[aa, bb, abb] and B=[aab, ba, b] 

Now for sequence 1, 2, 1, 3 first list will yield aabbaaabb and second list will yield same string aabbaaabb. So the solution to this PCP becomes 1, 2, 1, 3. Post Correspondence Problems can be represented in two ways: 

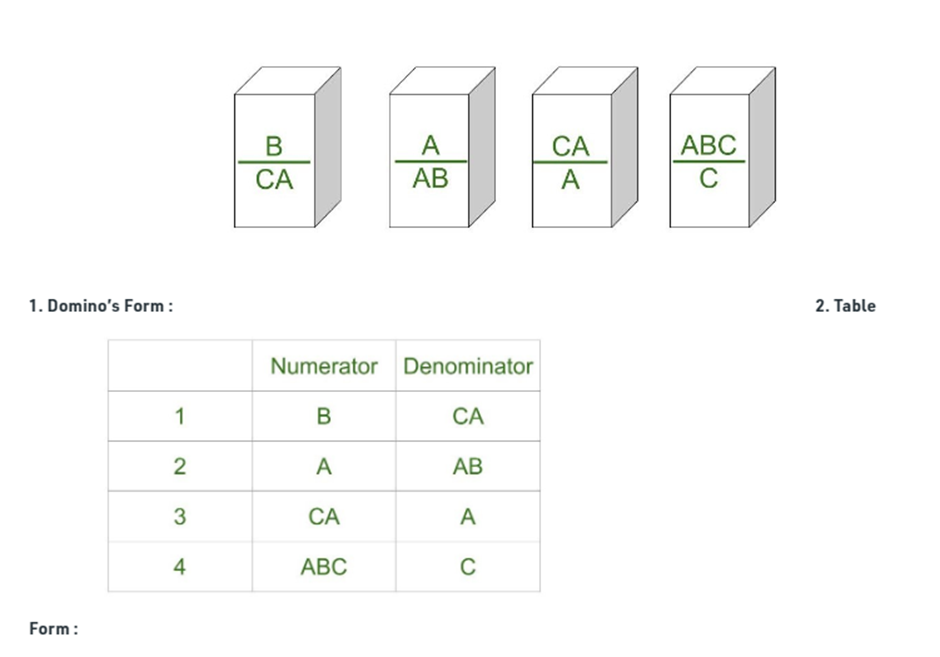
Lets consider following examples. Example-1:

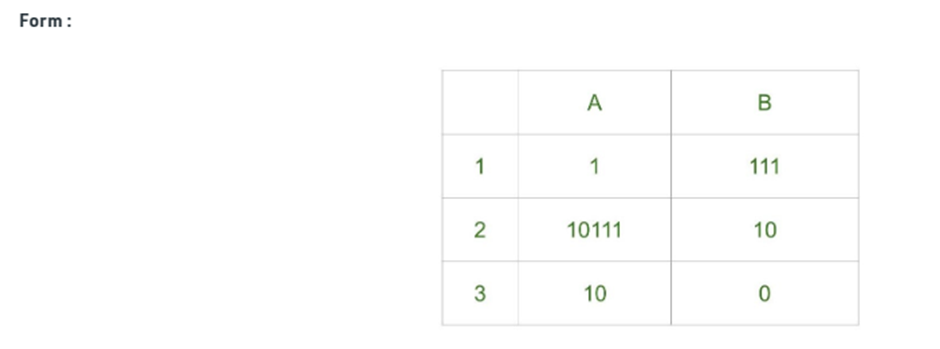
Explanation –

• Step-1: We will start with tile in which numerator and denominator are starting with same number, so we can start with either 1 or 2. Lets go with second tile, string made by numerator- 10111, string made by denominator is 10.
• Step-2: We need 1s in denominator to match 1s in numerator so we will go with first tile, string made by numerator is 10111 1, string made by denominator is 10 111.
• Step-3: There is extra 1 in numerator to match this 1 we will add first tile in sequence, string made by numerator is now 10111 1 1, string made by denominator is 10 111 111.
• Step-4: Now there is extra 1 in denominator to match it we will add third tile, string made by numerator is 10111 1 1 10, string made by denominator is 10 111 111 0.

Final Solution – 2 1 1 3

String made by numerators: 101111110

String made by denominators: 101111110

• As you can see, strings are same.

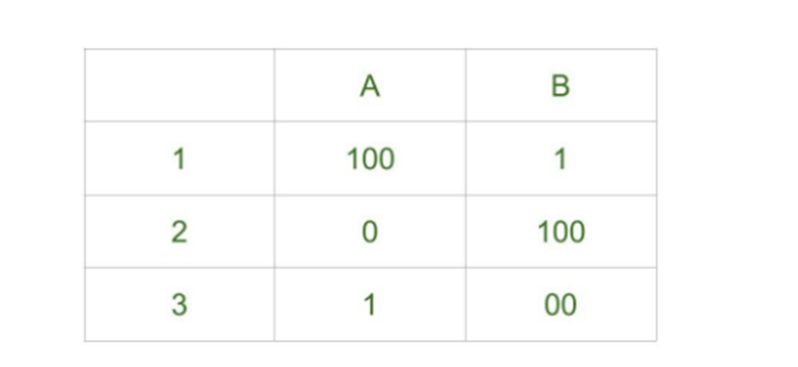
We can try unlimited combinations like one above but none of combination will lead us to solution, thus this problem does not have solution. Undecidability of Post Correspondence Problem : As theorem says that PCP is undecidable. That is, there is no particular algorithm that determines whether any Post Correspondence System has solution or not. Proof – We already know about undecidability of Turing Machine. If we are able to reduce Turing Machine to PCP then we will prove that PCP is undecidable as well. Consider Turing machine M to simulate PCP’s input string w can be represented as .

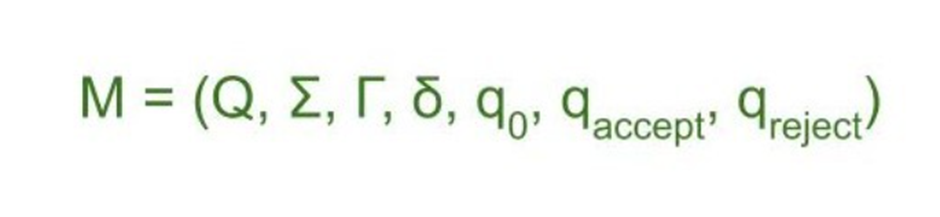
If there is match in input string w, then Turing machine M halts in accepting state. This halting state of Turing machine is acceptance problem A_TM. We know that acceptance problem A_TM is undecidable. Therefore PCP problem is also undecidable. To force simulation of M, we make 2 modifications to Turing Machine M and one change to our PCP problem.

1. M on input w can never attempt to move tape head beyond left end of input tape.
2. If input is empty string € we use _ .
3. PCP problem starts match with first domino [u1/v1] This is called Modified PCP problem.

MPCP = {[D] | D is instance of PCP starts with first domino}

Construction Steps –

1. Put [# / (#q0w1w2..wn#)] into D as first domino, where is instance of D is MPCP. A partial match is obtained in first domino is # at one face is same #symbol in other face.
2. Transition functions for Turing Machine M can have moves Left L, Right R. For every x, y z in tape alphabets and q, r in Q where q is not equal to q_reject. If transition(q, x) = (r, y, R) put domino [qx / by] into D and transition(q, x) =(r, y, L) put domino [zqx / rzy] into D.
3. For every tape alphabet x put [x / x] into D.To mark separation of each configurations put [# / #] and [# / _#] into D .
4. To read input alphabets x even after Turing Machine is accepting state put [xqa / qa] and [qax / qa]and [qa# / #] into D. These steps concludes construction of D.

Since this instance of MPCP, we need to convert this to PCP. So to convert to D, we consider below domino and strings matching.