Hill Climbing

Hill climbing is a local search algorithm used to find an optimal solution in optimization problems. It starts with an initial solution and iteratively improves it by making incremental changes. The algorithm explores neighboring solutions and moves towards the solution that maximizes or minimizes the objective function, depending on whether it is a maximization or minimization problem.

Here are the basic steps of the hill climbing algorithm:

1. Start with an initial solution.
2. Evaluate the current solution by calculating its objective function value.
3. Generate neighboring solutions by making small modifications to the current solution.
4. Evaluate the objective function value for each neighboring solution.
5. Select the best neighboring solution that improves the objective function the most (e.g., has a higher value for maximization problems or a lower value for minimization problems).
6. If the best neighboring solution is better than the current solution, move to that solution and repeat from step 2.
7. If the best neighboring solution is not better than the current solution, terminate and return the current solution as the output.

Hill climbing is a local search algorithm because it focuses on improving the current solution by exploring only the immediate neighbors. It does not maintain a global view of the search space and may get stuck in local optima or plateaus, where no immediate neighbors offer improvements. This limitation makes hill climbing suitable for simple optimization problems but less effective for complex problems with many local optima or large search spaces.

There are variations of hill climbing that address some of these limitations. For example, stochastic hill climbing introduces randomness by occasionally accepting worse solutions to escape local optima. Simulated annealing incorporates a temperature parameter that controls the acceptance of worse solutions, allowing for exploration in the early stages and exploitation in later stages. Genetic algorithms and evolutionary strategies use concepts from evolutionary biology, maintaining a population of solutions and applying operators like mutation and crossover to explore the search space.

Overall, hill climbing is a straightforward and intuitive optimization algorithm, but its effectiveness heavily depends on the problem’s characteristics and the landscape of the objective function.

Hill Climbing Algorithm in Artificial Intelligence

• Hill climbing algorithm is a local search algorithm which continuously moves in the direction of increasing elevation/value to find the peak of the mountain or best solution to the problem. It terminates when it reaches a peak value where no neighbor has a higher value.
• Hill climbing algorithm is a technique which is used for optimizing the mathematical problems. One of the widely discussed examples of Hill climbing algorithm is Traveling-salesman Problem in which we need to minimize the distance traveled by the salesman.
• It is also called greedy local search as it only looks to its good immediate neighbor state and not beyond that.
• A node of hill climbing algorithm has two components which are state and value.
• Hill Climbing is mostly used when a good heuristic is available.
• In this algorithm, we don’t need to maintain and handle the search tree or graph as it only keeps a single current state.

Features of Hill Climbing:

Following are some main features of Hill Climbing Algorithm:

• Generate and Test variant: Hill Climbing is the variant of Generate and Test method. The Generate and Test method produce feedback which helps to decide which direction to move in the search space.
• Greedy approach: Hill-climbing algorithm search moves in the direction which optimizes the cost.
• No backtracking: It does not backtrack the search space, as it does not remember the previous states.

State-space Diagram for Hill Climbing:

The state-space landscape is a graphical representation of the hill-climbing algorithm which is showing a graph between various states of algorithm and Objective function/Cost.

On Y-axis we have taken the function which can be an objective function or cost function, and state-space on the x-axis. If the function on Y-axis is cost then, the goal of search is to find the global minimum and local minimum. If the function of Y-axis is Objective function, then the goal of the search is to find the global maximum and local maximum.

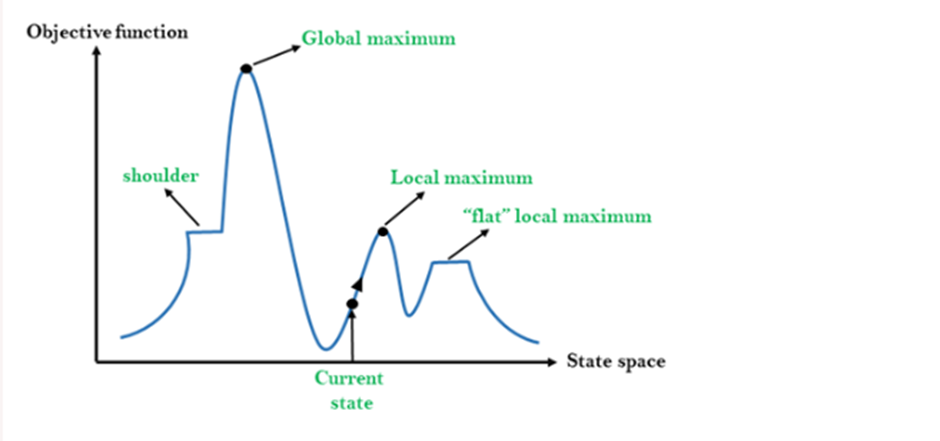
Different regions in the state space landscape:

Local Maximum: Local maximum is a state which is better than its neighbor states, but there is also another state which is higher than it.

Global Maximum: Global maximum is the best possible state of state space landscape. It has the highest value of objective function.

Current state: It is a state in a landscape diagram where an agent is currently present.

Flat local maximum: It is a flat space in the landscape where all the neighbor states of current states have the same value.

Shoulder: It is a plateau region which has an uphill edge.

Types of Hill Climbing Algorithm:

• Simple hill Climbing:
• Steepest-Ascent hill-climbing:
• Stochastic hill Climbing:

1. Simple Hill Climbing:

Simple hill climbing is the simplest way to implement a hill climbing algorithm. It only evaluates the neighbor node state at a time and selects the first one which optimizes current cost and set it as a current state. It only checks it’s one successor state, and if it finds better than the current state, then move else be in the same state. This algorithm has the following features:

• Less time consuming
• Less optimal solution and the solution is not guaranteed

Algorithm for Simple Hill Climbing:

• Step 1: Evaluate the initial state, if it is goal state then return success and Stop.
• Step 2: Loop Until a solution is found or there is no new operator left to apply.
• Step 3: Select and apply an operator to the current state.
• Step 4: Check new state:
  1. If it is goal state, then return success and quit.
  2. Else if it is better than the current state then assign new state as a current state.
  3. Else if not better than the current state, then return to step2.
• Step 5: Exit.

2. Steepest-Ascent hill climbing:

The steepest-Ascent algorithm is a variation of simple hill climbing algorithm. This algorithm examines all the neighboring nodes of the current state and selects one neighbor node which is closest to the goal state. This algorithm consumes more time as it searches for multiple neighbors

Algorithm for Steepest-Ascent hill climbing:

• Step 1: Evaluate the initial state, if it is goal state then return success and stop, else make current state as initial state.
• Step 2: Loop until a solution is found or the current state does not change.
  1. Let SUCC be a state such that any successor of the current state will be better than it.
  2. For each operator that applies to the current state:
     • Apply the new operator and generate a new state.
     • Evaluate the new state.
     • If it is goal state, then return it and quit, else compare it to the SUCC.
     • If it is better than SUCC, then set new state as SUCC.
     • If the SUCC is better than the current state, then set current state to SUCC.
• Step 5: Exit.

3. Stochastic hill climbing:

Stochastic hill climbing does not examine for all its neighbor before moving. Rather, this search algorithm selects one neighbor node at random and decides whether to choose it as a current state or examine another state.